TLS握手流程
TLS握手过程
HTTP 由于是明文传输,所谓的明文,就是说客户端与服务端通信的信息都是肉眼可见的,随意使用一个抓包工具都可以截获通信的内容。
所以安全上存在以下三个风险:
- 窃听风险,比如通信链路上可以获取通信内容,用户号容易没。
- 篡改风险,比如强制植入垃圾广告,视觉污染,用户眼容易瞎。
- 冒充风险,比如冒充淘宝网站,用户钱容易没。
HTTPS 在 HTTP 与 TCP 层之间加入了 TLS 协议,来解决上述的风险。
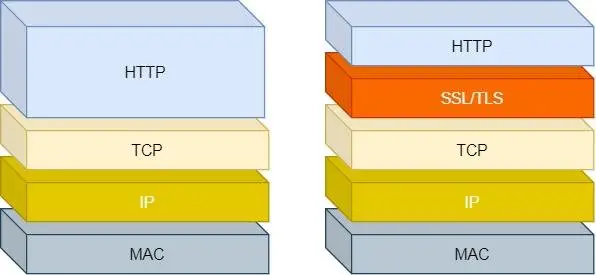
TLS 协议是如何解决 HTTP 的风险的呢?
- 信息加密:HTTP 交互信息是被加密的,第三方就无法被窃取。
- 校验机制:校验信息传输过程中是否有被第三方篡改过,如果被篡改过,则会有警告提示。
- 身份证书:证明淘宝是真的淘宝网。
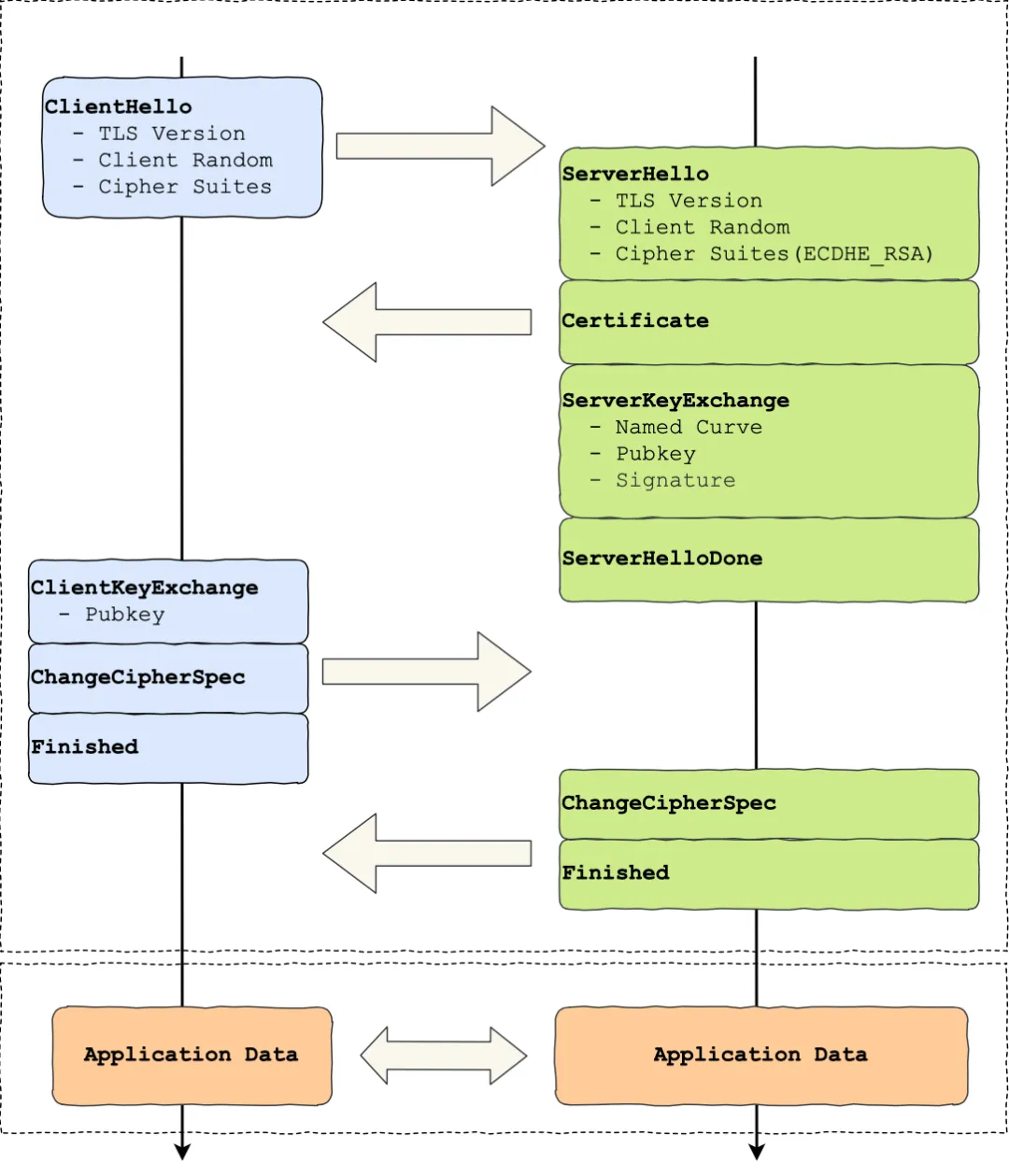
上图简要概述来 TLS 的握手过程,其中每一个「框」都是一个记录(record),记录是 TLS 收发数据的基本单位,类似于 TCP 里的 segment。多个记录可以组合成一个 TCP 包发送,所以通常经过「四个消息」就可以完成 TLS 握手,也就是需要 2个 RTT 的时延,然后就可以在安全的通信环境里发送 HTTP 报文,实现 HTTPS 协议。
所以可以发现,HTTPS 是应用层协议,需要先完成 TCP 连接建立,然后走 TLS 握手过程后,才能建立通信安全的连接。
事实上,不同的密钥交换算法,TLS 的握手过程可能会有一些区别。
这里先简单介绍下密钥交换算法,因为考虑到性能的问题,所以双方在加密应用信息时使用的是对称加密密钥,而对称加密密钥是不能被泄漏的,为了保证对称加密密钥的安全性,所以使用非对称加密的方式来保护对称加密密钥的协商,这个工作就是密钥交换算法负责的。
接下来,我们就以最简单的 RSA 密钥交换算法,来看看它的 TLS 握手过程。
RSA握手过程
传统的 TLS 握手基本都是使用 RSA 算法来实现密钥交换的,在将 TLS 证书部署服务端时,证书文件中包含一对公私钥,其中公钥会在 TLS 握手阶段传递给客户端,私钥则一直留在服务端,一定要确保私钥不能被窃取。
在 RSA 密钥协商算法中,客户端会生成随机密钥,并使用服务端的公钥加密后再传给服务端。根据非对称加密算法,公钥加密的消息仅能通过私钥解密,这样服务端解密后,双方就得到了相同的密钥,再用它加密应用消息。
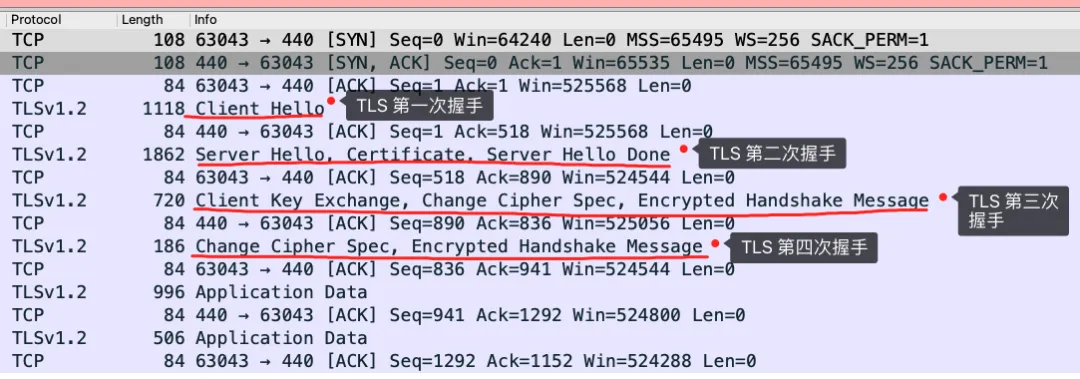
我用 Wireshark 工具抓了用 RSA 密钥交换的 TLS 握手过程,你可以从下面看到,一共经历来四次握手:
对应 Wireshark 的抓包,我也画了一幅图,你可以从下图很清晰地看到该过程:
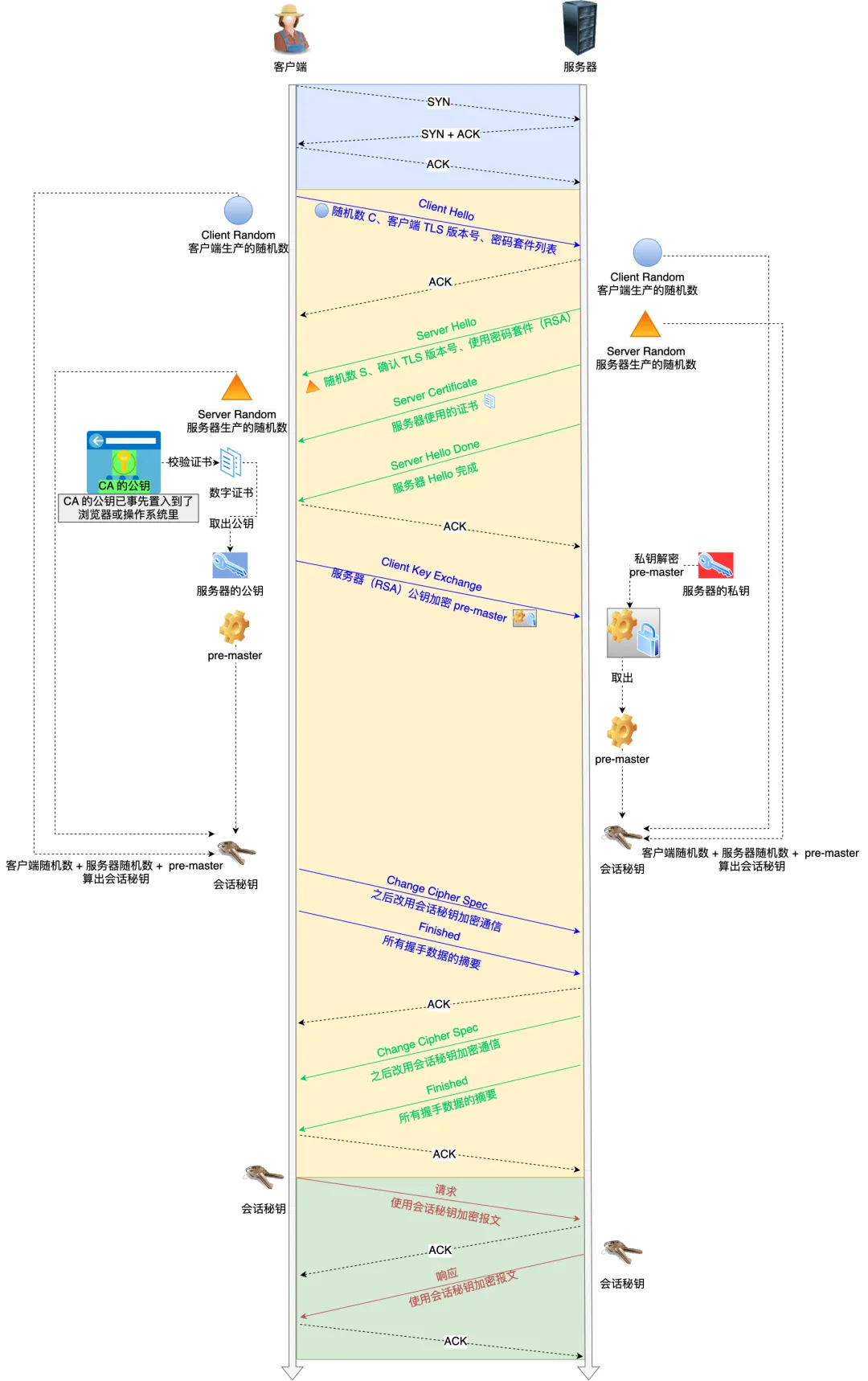
那么,接下来针对每一个 TLS 握手做进一步的介绍。
TLS第一次握手
客户端首先会发一个「Client Hello」消息,字面意思我们也能理解到,这是跟服务器「打招呼」。
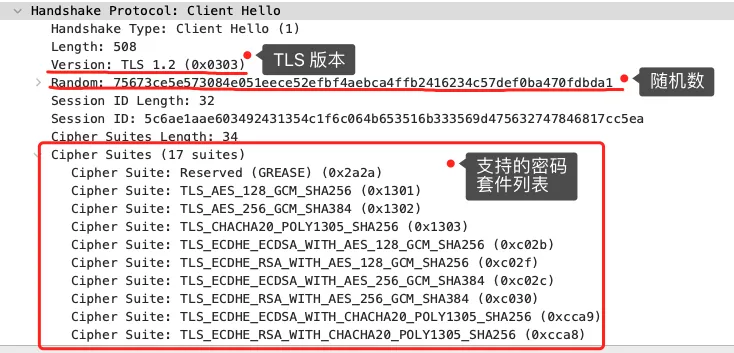
消息里面有客户端使用的TLS 版本号、支持的密码套件列表,以及生成的随机数(Client Random),这个随机数会被服务端保留,它是生成对称加密密钥的材料之一。
TLS第二次握手
当服务端收到客户端的「Client Hello」消息后,会确认 TLS 版本号是否支持,和从密码套件列表中选择一个密码套件,以及生成随机数(Server Random)。
接着,返回「Server Hello」消息,消息里面有服务器确认的 TLS 版本号,也给出了随机数(Server Random),然后从客户端的密码套件列表选择了一个合适的密码套件。
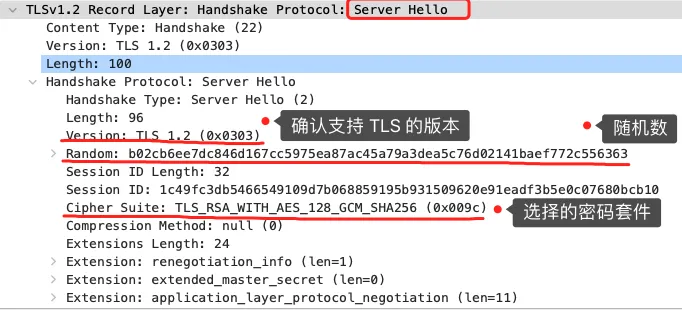
可以看到,服务端选择的密码套件是Cipher Suite: TLS_RSA_WITH_AES_128_GCM_SHA256。
这个密码套件看起来真让人头晕,好一大串,但是其实它是有固定格式和规范的。基本的形式是「密钥交换算法 + 签名算法 + 对称加密算法 + 摘要算法」, 一般 WITH 单词前面有两个单词,第一个单词是约定密钥交换的算法,第二个单词是约定证书的验证算法。比如刚才的密码套件的意思就是:
- 由于 WITH 单词只有一个 RSA,则说明握手时密钥交换算法和签名算法都是使用 RSA;
- 握手后的通信使用 AES 对称算法,密钥长度 128 位,分组模式是 GCM;
- 摘要算法 SHA256 用于消息认证和产生随机数;
就前面这两个客户端和服务端相互「打招呼」的过程,客户端和服务端就已确认了 TLS 版本和使用的密码套件,而且你可能发现客户端和服务端都会各自生成一个随机数,并且还会把随机数传递给对方。
那这个随机数有啥用呢?其实这两个随机数是后续作为生成「主密钥」和「会话密钥」的条件,所谓的主密钥,就是使用DH或者RSA等密钥交换算法得到的密钥(由预备主密钥、ClientHello random 和 ServerHello random 通过 PRF 函数生成的),而会话密钥就是数据传输时,所使用的对称加密密钥(由主密钥、SecurityParameters.server_random 和 SecurityParameters.client_random 通过 PRF 函数来生成)。
然后,服务端为了证明自己的身份,会发送「Server Certificate」给客户端,这个消息里含有数字证书。
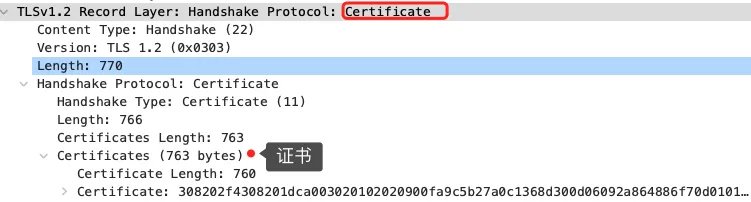
随后,服务端发了「Server Hello Done」消息,目的是告诉客户端,我已经把该给你的东西都给你了,本次打招呼完毕。

客户端验证证书
在这里刹个车,客户端拿到了服务端的数字证书后,要怎么校验该数字证书是真实有效的呢?
数字证书和CA机构
在说校验数字证书是否可信的过程前,我们先来看看数字证书是什么,一个数字证书通常包含了:
- 公钥;
- 持有者信息;
- 证书认证机构(CA)的信息;
- CA 对这份文件的数字签名及使用的算法;
- 证书有效期;
- 还有一些其他额外信息;
那数字证书的作用,是用来认证公钥持有者的身份,以防止第三方进行冒充。说简单些,证书就是用来告诉客户端,该服务端是否是合法的,因为只有证书合法,才代表服务端身份是可信的。
我们用证书来认证公钥持有者的身份(服务端的身份),那证书又是怎么来的?又该怎么认证证书呢?
为了让服务端的公钥被大家信任,服务端的证书都是由 CA (Certificate Authority,证书认证机构)签名的,CA 就是网络世界里的公安局、公证中心,具有极高的可信度,所以由它来给各个公钥签名,信任的一方签发的证书,那必然证书也是被信任的。
之所以要签名,是因为签名的作用可以避免中间人在获取证书时对证书内容的篡改。
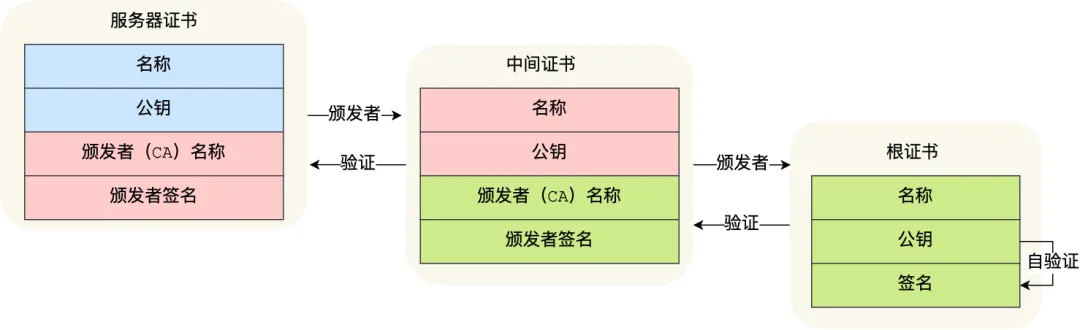
数字证书签发和验证流程
如下图图所示,为数字证书签发和验证流程:
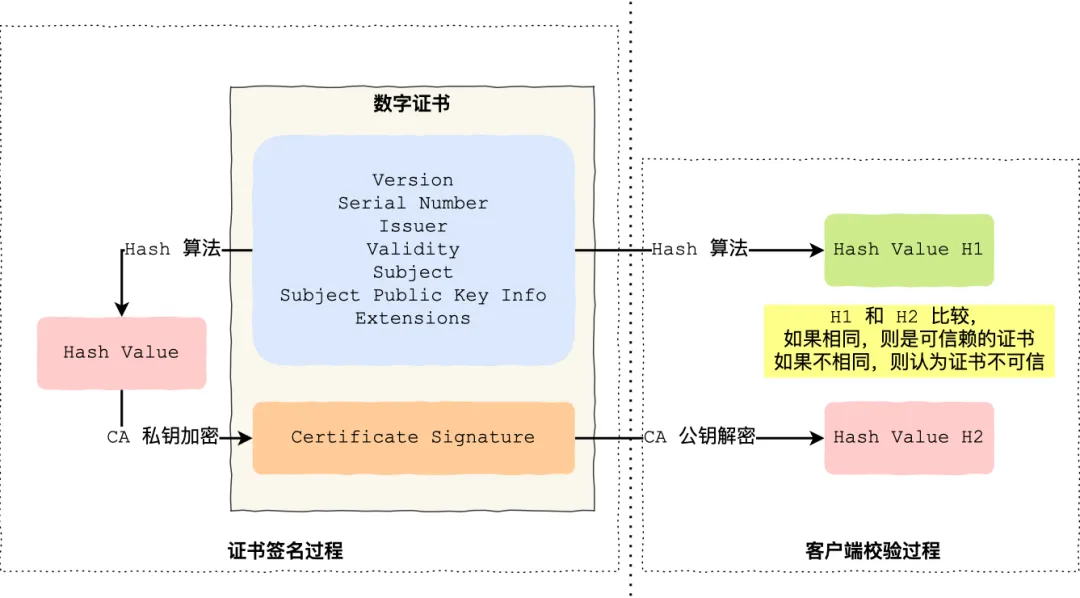
CA 签发证书的过程,如上图左边部分:
- 首先 CA 会把持有者的公钥、用途、颁发者、有效时间等信息打成一个包,然后对这些信息进行 Hash 计算,得到一个 Hash 值;
- 然后 CA 会使用自己的私钥将该 Hash 值加密,生成 Certificate Signature,也就是 CA 对证书做了签名;
- 最后将 Certificate Signature 添加在文件证书上,形成数字证书;
客户端校验服务端的数字证书的过程,如上图右边部分:
- 首先客户端会使用同样的 Hash 算法获取该证书的 Hash 值 H1;
- 通常浏览器和操作系统中集成了 CA 的公钥信息,浏览器收到证书后可以使用 CA 的公钥解密 Certificate Signature 内容,得到一个 Hash 值 H2 ;
- 最后比较 H1 和 H2,如果值相同,则为可信赖的证书,否则则认为证书不可信。
证书链
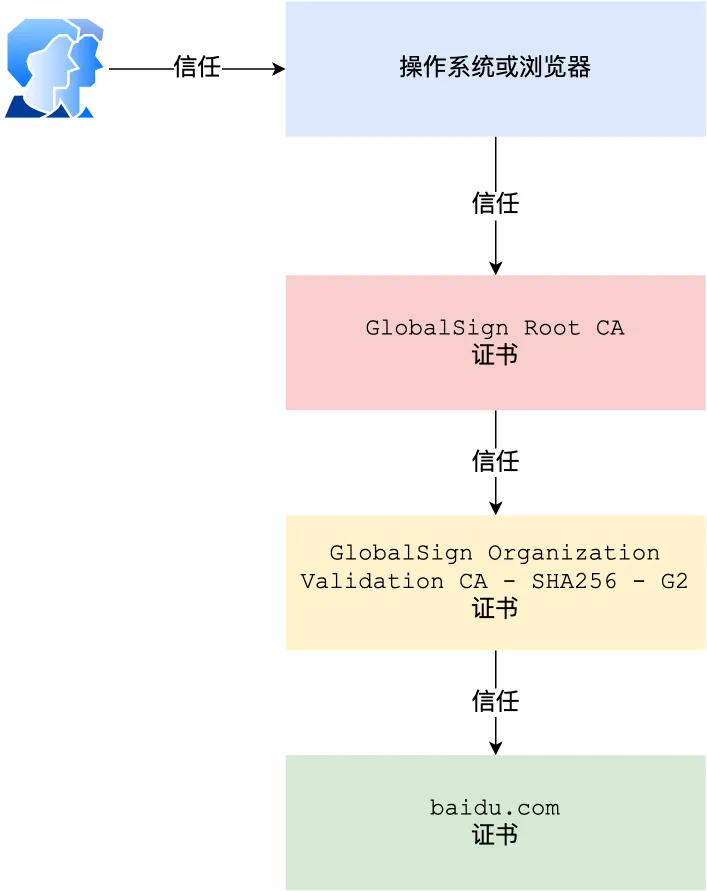
但事实上,证书的验证过程中还存在一个证书信任链的问题,因为我们向 CA 申请的证书一般不是根证书签发的,而是由中间证书签发的,比如百度的证书,从下图你可以看到,证书的层级有三级:

对于这种三级层级关系的证书的验证过程如下:
- 客户端收到 baidu.com 的证书后,发现这个证书的签发者不是根证书,就无法根据本地已有的根证书中的公钥去验证 baidu.com 证书是否可信。于是,客户端根据 baidu.com 证书中的签发者,找到该证书的颁发机构是
GlobalSign Organization Validation CA - SHA256 - G2,然后向 CA 请求该中间证书。 - 请求到证书后发现
GlobalSign Organization Validation CA - SHA256 - G2证书是由GlobalSign Root CA签发的,由于GlobalSign Root CA没有再上级签发机构,说明它是根证书,也就是自签证书。应用软件会检查此证书有否已预载于根证书清单上,如果有,则可以利用根证书中的公钥去验证GlobalSign Organization Validation CA - SHA256 - G2证书,如果发现验证通过,就认为该中间证书是可信的。 GlobalSign Organization Validation CA - SHA256 - G2证书被信任后,可以使用GlobalSign Organization Validation CA - SHA256 - G2证书中的公钥去验证 baidu.com 证书的可信性,如果验证通过,就可以信任 baidu.com 证书。
在这四个步骤中,最开始客户端只信任根证书 GlobalSign Root CA 证书的,然后 GlobalSign Root CA 证书信任 GlobalSign Organization Validation CA - SHA256 - G2 证书,而 GlobalSign Organization Validation CA - SHA256 - G2 证书又信任 baidu.com 证书,于是客户端也信任 baidu.com 证书。
总括来说,由于用户信任 GlobalSign ,所以由 GlobalSign 所担保的 baidu.com 可以被信任,另外由于用户信任操作系统或浏览器的软件商,所以由软件商预载了根证书的 GlobalSign 都可被信任。
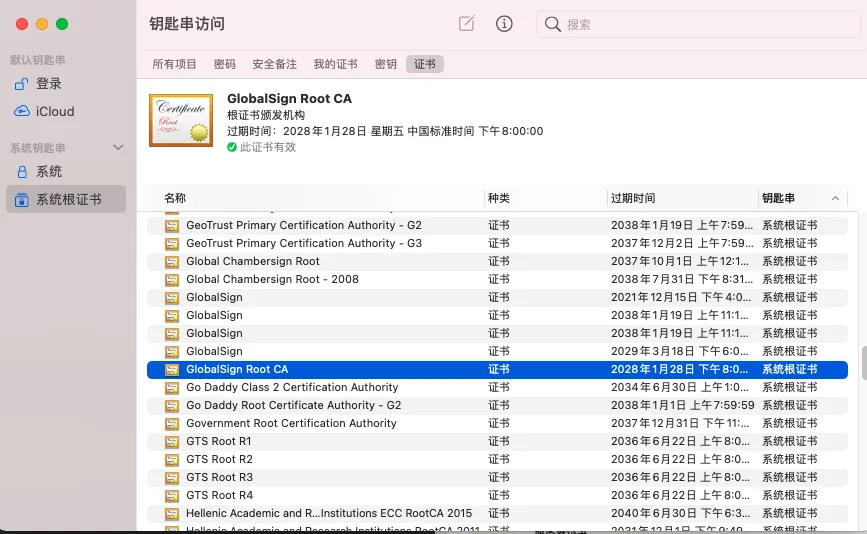
操作系统里一般都会内置一些根证书,比如我的 MAC 电脑里内置的根证书有这么多:
这样的一层层地验证就构成了一条信任链路,整个证书信任链验证流程如下图所示:
最后一个问题,为什么需要证书链这么麻烦的流程?Root CA 为什么不直接颁发证书,而是要搞那么多中间层级呢?
这是为了确保根证书的绝对安全性,将根证书隔离地越严格越好,不然根证书如果失守了,那么整个信任链都会有问题。
TLS第三次握手
客户端验证完证书后,认为可信则继续往下走。接着,客户端就会生成一个新的随机数 (pre-master),用服务器的 RSA 公钥加密该随机数,通过「Change Cipher Key Exchange」消息传给服务端。
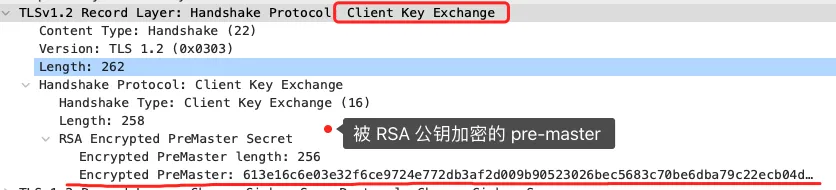
服务端收到后,用 RSA 私钥解密,得到客户端发来的随机数 (pre-master)。
至此,客户端和服务端双方都共享了三个随机数,分别是 Client Random、Server Random、pre-master。
于是,双方根据已经得到的三个随机数,生成主密钥(Master Secret),它是对称密钥,用于生成会话密钥对后续的 HTTP 请求/响应的数据加解密。
生成完会话密钥后,然后客户端发一个「Change Cipher Spec」,告诉服务端开始使用加密方式发送消息。

然后,客户端再发一个「Encrypted Handshake Message(Finishd)」消息,把之前所有发送的数据做个摘要,再用会话密钥(master secret)加密一下,让服务器做个验证,验证加密通信是否可用和之前握手信息是否有被中途篡改过。

可以发现,「Change Cipher Spec」之前传输的 TLS 握手数据都是明文,之后都是对称密钥加密的密文。
TLS第四次握手
服务器也是同样的操作,发「Change Cipher Spec」和「Encrypted Handshake Message」消息,如果双方都验证加密和解密没问题,那么握手正式完成。
最后,就用「会话密钥」加解密 HTTP 请求和响应了。
RSA算法的缺陷
使用 RSA 密钥协商算法的最大问题是不支持前向保密。因为客户端传递随机数(用于生成对称加密密钥的条件之一)给服务端时使用的是公钥加密的,服务端收到到后,会用私钥解密得到随机数。所以一旦服务端的私钥泄漏了,过去被第三方截获的所有 TLS 通讯密文都会被破解。
为了解决这一问题,于是就有了 DH 密钥协商算法,这里简单介绍它的工作流程。
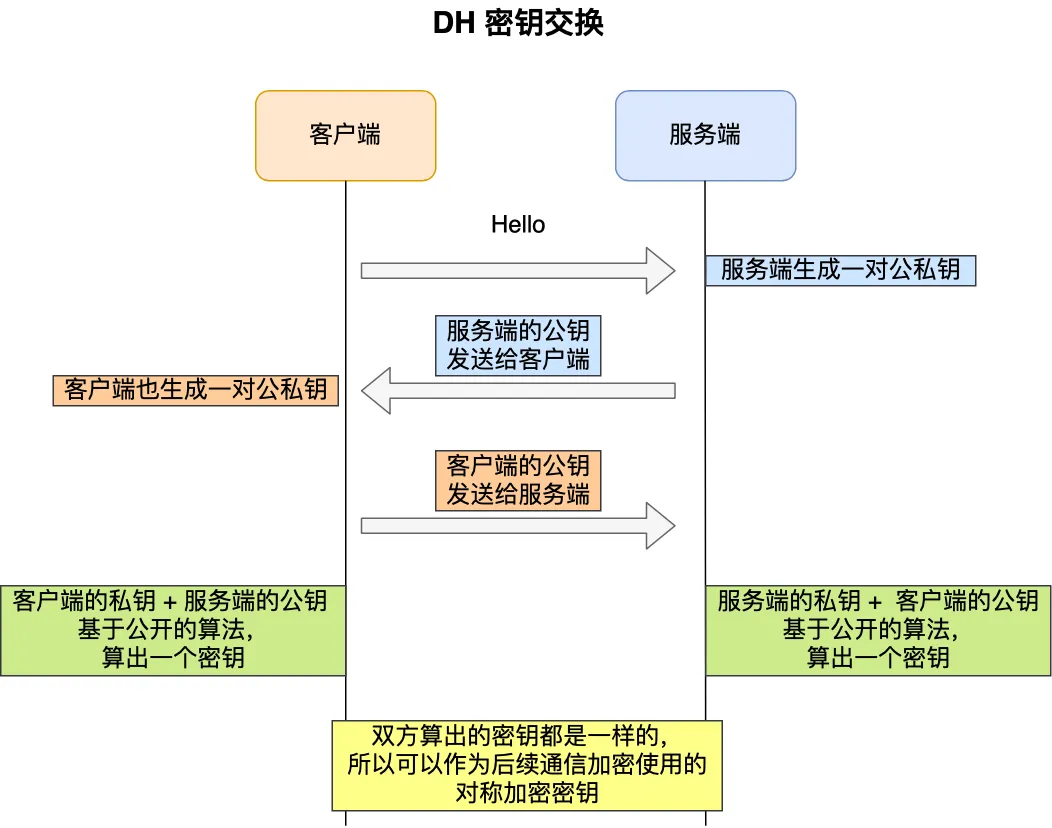
客户端和服务端各自会生成随机数,并以此作为私钥,然后根据公开的 DH 计算公示算出各自的公钥,通过 TLS 握手双方交换各自的公钥,这样双方都有自己的私钥和对方的公钥,然后双方根据各自持有的材料算出一个随机数,这个随机数的值双方都是一样的,这就可以作为后续对称加密时使用的密钥。
DH 密钥交换过程中,私钥每次都是随机生成的,因此实现了前向保密。
离散对数
ECDHE 密钥协商算法是 DH 算法演进过来的,所以我们先从 DH 算法说起。DH 算法是非对称加密算法, 因此它可以用于密钥交换,该算法的核心数学思想是离散对数。离散对数是「离散 + 对数」的两个数学概念的组合,所以我们先来复习一遍对数。要说起对数,必然要说指数,因为它们是互为反函数,指数就是幂运算,对数是指数的逆运算。举个栗子,如果以 2 作为底数,那么指数和对数运算公式,如下所示:
| 指数运算 | 对数运算 | |
|---|---|---|
| 32的对数 | \(32 = 2^5\) | \(5 = log_2^{32}\) |
| 64的对数 | \(64 = 2^6\) | \(6 = log_2^{64}\) |
而离散对数其实本质上与常规的对数运算一样,都是求解\(a^x = b\)当中的解\(x\),他们的核心不同点在于,两个运算所处的数学结构不同(即群不同)。传统的对数运算主要定义在实数域或者复数域等连续域当中,而离散对数通常定义在有限的离散群当中(模运算群,椭圆曲线群),这就导致了离散对数的计算复杂度非常高(尤其在大素数模数或椭圆曲线群中)。
离散对数的一个实例
离散对数最简单的设置之一是组\((\mathbb{Z}_p)^x\)。这是以素数 \(p\) 为模的一个乘法组。它的元素是以 \(p\) 为模的同余类,并且两个元素的组乘积可以在元素的普通整数乘法运算之后再模 \(p\) 得到。
上述组中,一个数的 \(k\) 次幂可以通过将其 \(k\) 次幂作为整数求出之后,再除以 \(p\) 求出余数的方式来计算。当涉及的数字很大时,在计算过程中多次减小模 \(p\) 会更加具有效率。不管使用哪种特定算法,都会调用该操作:模幂运算。例如,研究\((\mathbb{Z}_{17})^x\)。为了计算该组中的\(3^4\) ,计算得到\(3^4 = 81\),然后用\(81\)除以\(17\),得到大小为\(13\)的余数。因此在组\((\mathbb{Z}_{17})^x\)中\(3^4 = 13\)。
离散对数就是逆运算。例如,研究关于 \(k\) 的方程\(3^k ≡ 13 (mod\ 17)\)。在上面的例子中,一个解是 \(k = 4\),但是这不是唯一的解。由于\(3^{16} ≡1(mod\ 17)\)-遵循费马小定理-因此,如果 \(n\) 是一个整数,那么就有\(3^{4+16n} ≡ 3^4 × (3^{16})^n ≡ 13 × 1^n ≡ 13 (mod\ 17)\)。因此,这个方程有无穷多个\(4 + 16n\)形式的解。此外,因为\(16\)是满足\(3^m ≡ 1 (mod\ 17)\)的最小正整数 \(m\) ,所以这些是方程仅有的解。等价地,所有可能解的集合可以由一个约束条件来表示,该约束条件为 \(k ≡ 4 (mod\ 16)\)。
DH算法
认识了离散对数,我们来看看 DH 算法是如何密钥交换的。现假设小红和小明约定使用 DH 算法来交换密钥,那么基于离散对数,小红和小明需要先确定模数和底数作为算法的参数,这两个参数是公开的,用 \(P\) 和 \(G\) 来代称。
然后小红和小明各自生成一个随机整数作为私钥,双方的私钥要各自严格保管,不能泄漏,小红的私钥用 \(a\) 代称,小明的私钥用 \(b\) 代称。
现在小红和小明双方都有了 \(P\) 和 \(G\) 以及各自的私钥,于是就可以计算出公钥:
- 小红的公钥记作 \(A\),\(A = G ^ a ( mod\ P )\);
- 小明的公钥记作 \(B\),\(B = G ^ b ( mod\ P )\);
\(A\) 和 \(B\) 也是公开的,因为根据离散对数的原理,从真数(\(A\) 和 \(B\))反向计算对数 \(a\) 和 \(b\) 是非常困难的,至少在现有计算机的计算能力是无法破解的,如果量子计算机出来了,那就有可能被破解,当然如果量子计算机真的出来了,那么密钥协商算法就要做大的升级了。
双方交换各自 DH 公钥后,小红手上共有 \(5\) 个数:\(P\)、\(G\)、\(a\)、\(A\)、\(B\),小明手上也同样共有 5 个数:\(P\)、\(G\)、\(b\)、\(B\)、\(A\)。然后小红执行运算:\(B ^ a ( mod\ P )\),其结果为 \(K\),因为离散对数的幂运算有交换律,所以小明执行运算:\(A ^ b ( mod\ P )\),得到的结果也是 \(K\)。
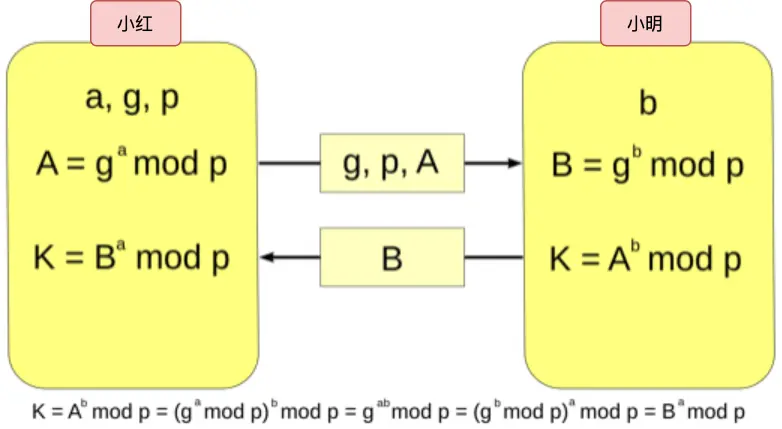
这个 \(K\) 就是小红和小明之间用的对称加密密钥,可以作为会话密钥使用(但是通常不这么做)。
可以看到,整个密钥协商过程中,小红和小明公开了 \(4\) 个信息:\(P\)、\(G\)、\(A\)、\(B\),其中 \(P\)、\(G\) 是算法的参数,\(A\) 和 \(B\) 是公钥,而 \(a\)、\(b\) 是双方各自保管的私钥,黑客无法获取这 \(2\) 个私钥,因此黑客只能从公开的 \(P\)、\(G\)、\(A\)、\(B\) 入手,计算出离散对数(私钥)。
前面也多次强调, 根据离散对数的原理,如果 \(P\) 是一个大数,在现有的计算机的计算能力是很难破解出 私钥 \(a\)、\(b\) 的,破解不出私钥,也就无法计算出主密钥,因此 DH 密钥交换是安全的。
DHE算法
根据私钥生成的方式,DH 算法分为两种实现:
- static DH 算法,这个是已经被废弃了。
- DHE 算法,现在常用的。
static DH 算法里有一方的私钥是静态的,也就说每次密钥协商的时候有一方的私钥都是一样的,一般是服务器方固定,即 a 不变,客户端的私钥则是随机生成的。
于是,DH 交换密钥时就只有客户端的公钥是变化,而服务端公钥是不变的,那么随着时间延长,黑客就会截获海量的密钥协商过程的数据,因为密钥协商的过程有些数据是公开的,黑客就可以依据这些数据暴力破解出服务器的私钥,然后就可以计算出主密钥了,于是之前截获的加密数据会被破解,所以 static DH 算法不具备前向安全性。
既然固定一方的私钥有被破解的风险,那么干脆就让双方的私钥在每次密钥交换通信时,都是随机生成的、临时的,这个方式也就是 DHE 算法,E 全称是 ephemeral(临时性的)。所以,即使有个牛逼的黑客破解了某一次通信过程的私钥,其他通信过程的私钥仍然是安全的,因为每个通信过程的私钥都是没有任何关系的,都是独立的,这样就保证了「前向安全」。
ECDHE算法
DHE 算法由于计算性能不佳,因为需要做大量的乘法,为了提升 DHE 算法的性能,所以就出现了现在广泛用于密钥交换算法 —— ECDHE 算法。
ECDHE 算法是在 DHE 算法的基础上利用了 ECC 椭圆曲线特性,可以用更少的计算量计算出公钥,以及最终的会话密钥。
小红和小明使用 ECDHE 密钥交换算法的过程:
- 双方事先确定好使用哪种椭圆曲线,和曲线上的基点 \(G\),这两个参数都是公开的;
- 双方各自随机生成一个随机数作为私钥\(d\),并与基点 \(G\)相乘得到公钥\(Q\)(\(Q = dG\)),此时小红的公私钥为 \(Q_1\) 和 \(d_1\),小明的公私钥为 \(Q_2\) 和 \(d_2\);
- 双方交换各自的公钥,最后小红计算点\((x_1,y_1) = d_1Q_2\),小明计算点\((x_2,y_2) = d_2Q_1\),由于椭圆曲线上是可以满足乘法交换和结合律,所以 \(d_1Q_2 = d_1d_2G = d_2d_1G = d_2Q_1\) ,因此双方的 \(x\) 坐标是一样的,所以它是共享密钥,也就是预主密钥。
这个过程中,双方的私钥都是随机、临时生成的,都是不公开的,即使根据公开的信息(椭圆曲线、公钥、基点 G)也是很难计算出椭圆曲线上的离散对数(私钥)。
ECDHE握手过程
知道了 ECDHE 算法基本原理后,我们就结合实际的情况来看看。 我用 Wireshark 工具抓了用 ECDHE 密钥协商算法的 TSL 握手过程,可以看到是四次握手:
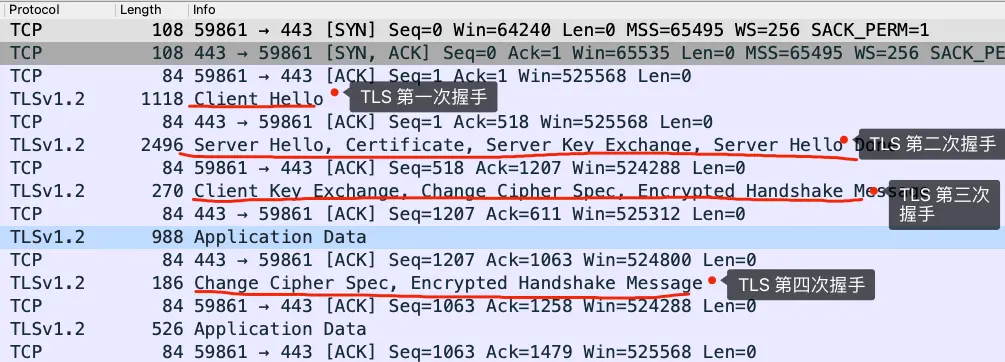
细心的小伙伴应该发现了,使用了 ECDHE,在 TLS 第四次握手前,客户端就已经发送了加密的 HTTP 数据,而对于 RSA 握手过程,必须要完成 TLS 四次握手,才能传输应用数据。
所以,ECDHE 相比 RSA 握手过程省去了一个消息往返的时间,这个有点「抢跑」的意思,它被称为是「TLS False Start」,跟「TCP Fast Open」有点像,都是在还没连接完全建立前,就发送了应用数据,这样便提高了传输的效率。
其详细的通信流程图如下:
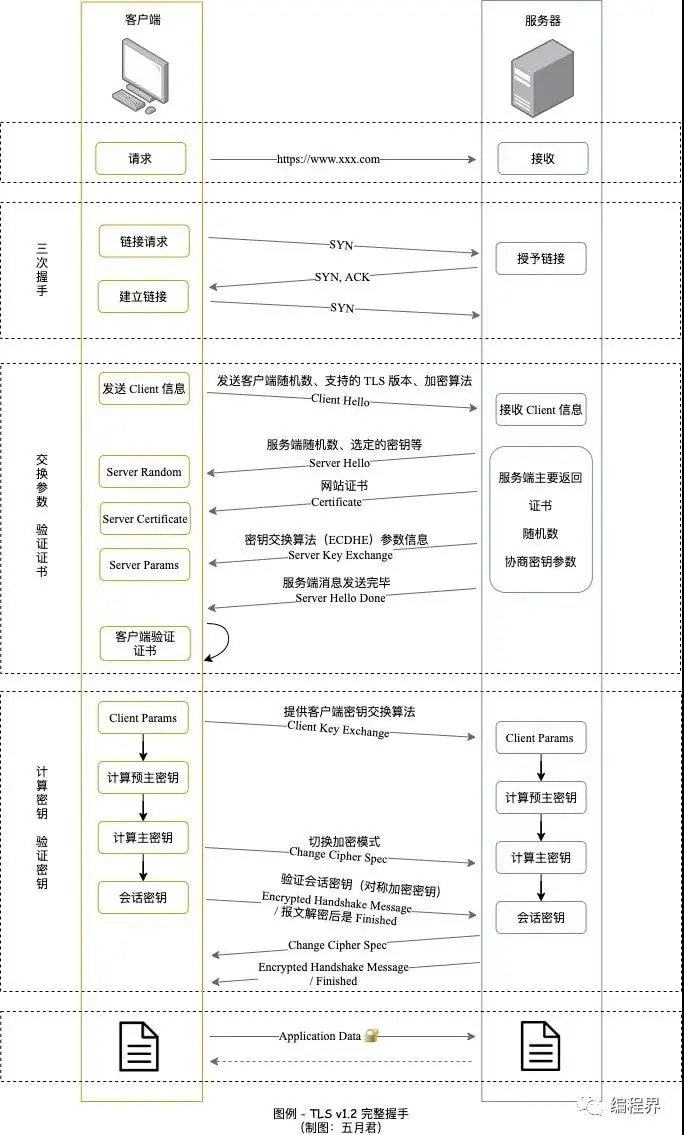
TLS第一次握手
客户端首先会发一个「Client Hello」消息,消息里面有客户端使用的 TLS 版本号、支持的密码套件列表,以及生成的随机数(Client Random)。
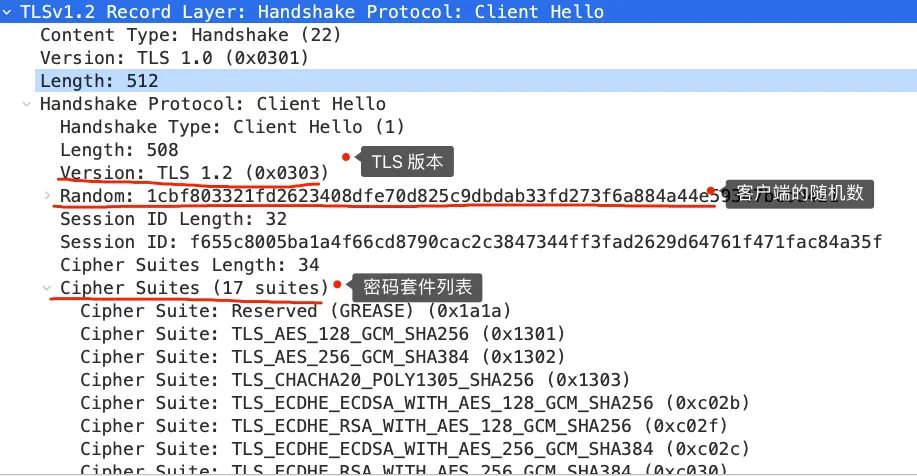
TLS第二次握手
服务端收到客户端的「打招呼」,同样也要回礼,会返回「Server Hello」消息,消息面有服务器确认的 TLS 版本号,也给出了一个随机数(Server Random),然后从客户端的密码套件列表选择了一个合适的密码套件。
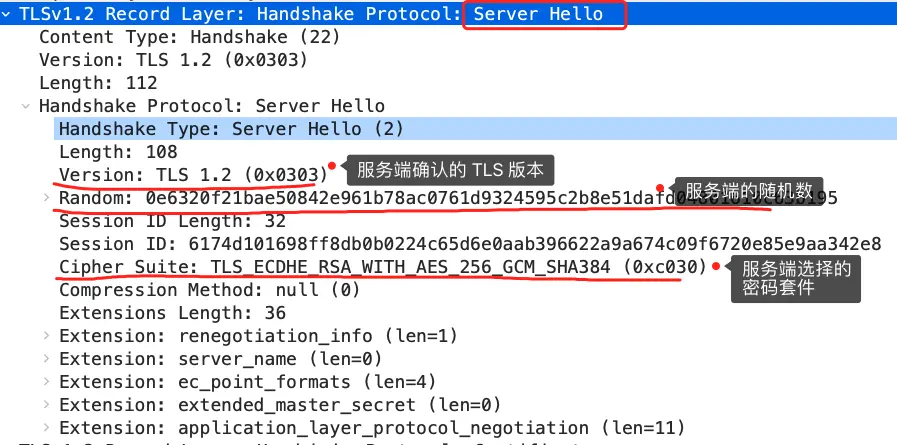
不过,这次选择的密码套件就和 RSA 不一样了,我们来分析一下这次的密码套件的意思。
「TLS_ECDHE_RSA_WITH_AES_256_GCM_SHA384」
- 密钥协商算法使用 ECDHE;
- 签名算法使用 RSA;
- 握手后的通信使用 AES 对称算法,密钥长度 256 位,分组模式是 GCM;
- 摘要算法使用 SHA384;
接着,服务端为了证明自己的身份,发送「Certificate」消息,会把证书也发给客户端。
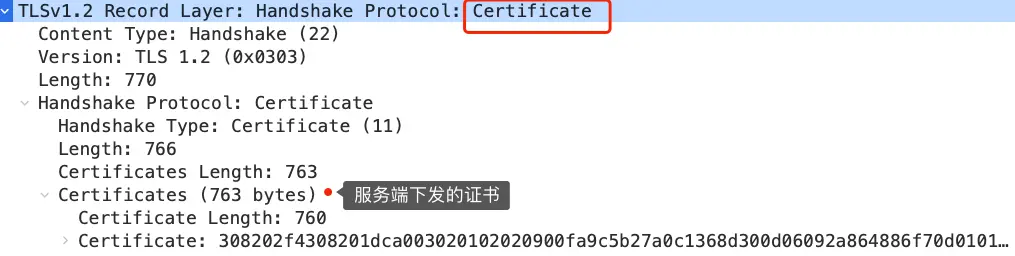
这一步就和 RSA 握手过程有很大到区别了,因为服务端选择了 ECDHE 密钥协商算法,所以会在发送完证书后,发送「Server Key Exchange」消息。
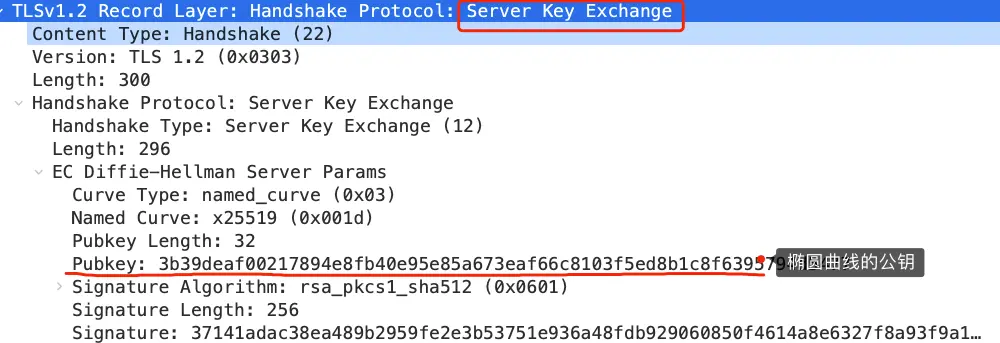
这个过程服务器做了三件事:
- 选择了名为 named_curve 的椭圆曲线,选好了椭圆曲线相当于椭圆曲线基点 \(G\) 也定好了,这些都会公开给客户端;
- 生成随机数作为服务端椭圆曲线的私钥,保留到本地;
- 根据基点 \(G\) 和私钥计算出服务端的椭圆曲线公钥,这个会公开给客户端。
为了保证这个椭圆曲线的公钥不被第三方篡改,服务端会用 RSA 签名算法给服务端的椭圆曲线公钥做个签名。
随后,就是「Server Hello Done」消息,服务端跟客户端表明:“这些就是我提供的信息,打招呼完毕”。

至此,TLS 两次握手就已经完成了,目前客户端和服务端通过明文共享了这几个信息:Client Random、Server Random 、使用的椭圆曲线、椭圆曲线基点 G、服务端椭圆曲线的公钥,这几个信息很重要,是后续生成主密钥和会话密钥的材料。
TLS第三次握手
客户端收到了服务端的证书后,自然要校验证书是否合法,如果证书合法,那么服务端到身份就是没问题的。校验证书到过程,会走证书链逐级验证,确认证书的真实性,再用证书的公钥验证签名,这样就能确认服务端的身份了,确认无误后,就可以继续往下走。
客户端会生成一个随机数作为客户端椭圆曲线的私钥,然后再根据服务端前面给的信息,生成客户端的椭圆曲线公钥,然后用「Client Key Exchange」消息发给服务端。
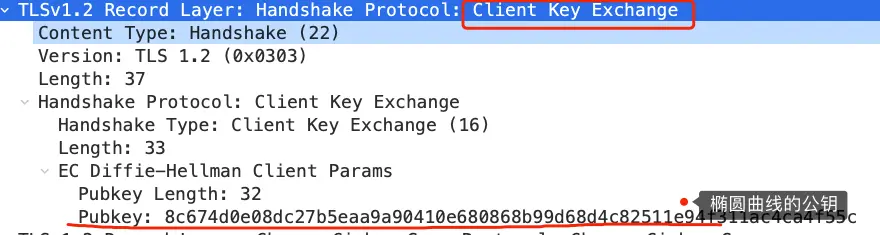
至此,双方都有对方的椭圆曲线公钥、自己的椭圆曲线私钥、椭圆曲线基点 \(G\)。于是,双方都就计算出点\((x,y)\),其中 \(x\) 坐标值双方都是一样的,前面说 ECDHE 算法时候,说 \(x\) 可以作为会话密钥,但实际应用中,\(x\) 还不是最终的会话密钥。
还记得 TLS 握手阶段,客户端和服务端都会生成了一个随机数传递给对方吗?最终的主密钥,就是用「客户端随机数 + 服务端随机数 + x(ECDHE 算法算出的共享密钥) 」三个材料生成的。之所以这么麻烦,是因为 TLS 设计者不信任客户端或服务器「伪随机数」的可靠性,为了保证真正的完全随机,把三个不可靠的随机数混合起来,那么「随机」的程度就非常高了,安全性更高。然后再利用主密钥,使用PRF算法得到会话密钥
算好会话密钥后,客户端会发一个「Change Cipher Spec」消息,告诉服务端后续改用对称算法加密通信。

接着,客户端会发「Encrypted Handshake Message」消息,把之前发送的数据做一个摘要,再用对称密钥加密一下,让服务端做个验证,验证下本次生成的对称密钥是否可以正常使用。

TLS第四次握手
最后,服务端也会有一个同样的操作,发「Change Cipher Spec」和「Encrypted Handshake Message」消息,如果双方都验证加密和解密没问题,那么握手正式完成。于是,就可以正常收发加密的 HTTP 请求和响应了。
总结
RSA 和 ECDHE 握手过程的区别:
- RSA 密钥协商算法「不支持」前向保密,ECDHE 密钥协商算法「支持」前向保密;
- 使用了 RSA 密钥协商算法,TLS 完成四次握手后,才能进行应用数据传输,而对于 ECDHE 算法,客户端可以不用等服务端的最后一次 TLS 握手,就可以提前发出加密的 HTTP 数据,节省了一个消息的往返时间(RTT);
- 使用 ECDHE, 在 TLS 第 2 次握手中,会出现服务器端发出的「Server Key Exchange」消息,而 RSA 握手过程没有该消息(握手流程上的区别主要在这里);
